4.3: Completing the View-Projection Matrix
In the previous section, we built the View-Projection matrix without translation. now it’s time to dive into the function that actually puts everything together into the full View-Projection matrix.
Remember the final call to sub_7FBF10 in the previous function:
return sub_7FBF10(camStruct, &v15, v16);
- So the first Argument a1 is the camStruct
- Second argument a2 is the CameraPostion
- Third argument a3 is the View-Projection Matrix without Translation
Lets rename as such and continue.
Matrix Loading into Memory:
- Loads Camera Position into CamStruct + 0x550
- Loads VP Matrix (No_translation) into CamStruct + 0x430
Matrix Inverse
We wont dive into this but this basically Makes an inverse Matrix of ViewProj_No_t and saves it to a pointer Camstruct + 0x4B0
We will be skipping functions and instructions that dont seem interesting as it is out of scope for this blog
Making sense:
Let’s Try and make sense of this and rename all relevent variables.
Here is a renamed and cleaned up version.
Another redundant SIMD math function
You might have noticed another redundant SIMD function here.
What does this code do?
Basically it takes CamPos [x,y,z,w] where w was already ‘1’ and negates it and keeps it ‘1’ at ‘w’.
CamPos [x,y,z,1] = [-x,-y,-z,1]
There is no reason for such a simple negation to have this many SIMD operations here and are mostly redundant.
Negated Camera position Multiplication with ViewProjection Matrix
I’ve already shown how vec4 × mat4 works in SIMD in my previous post, so I won’t re-explain it here. This is the same thing again.
it’s just multiplying the negated camera position (with w=1) by the ViewProjection matrix without translation. The result is effectively
adding the translation into the VP matrix which did not have translation.
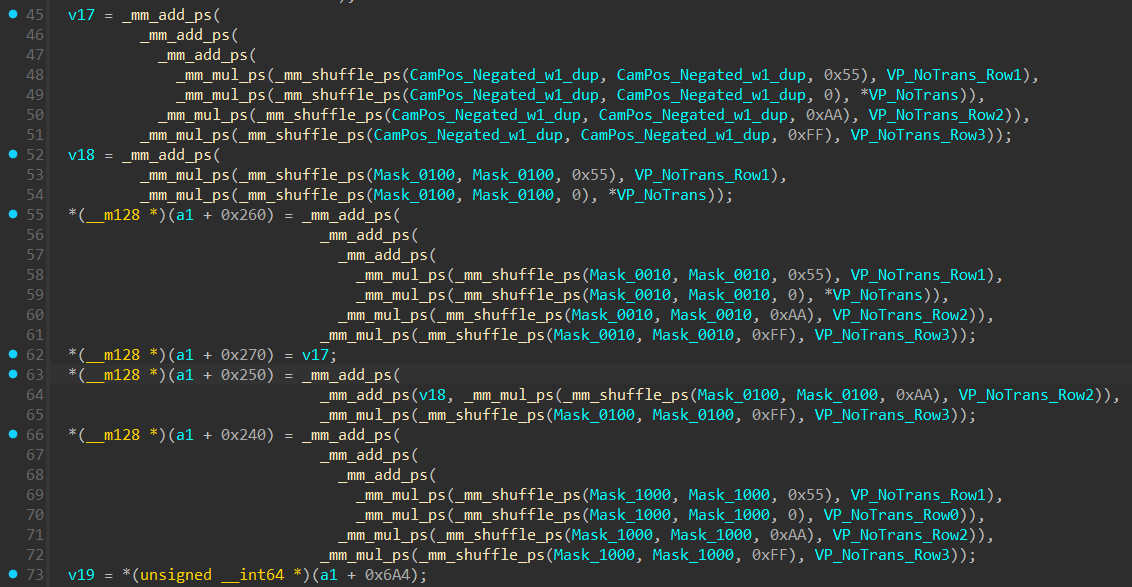
Now lets make sense of the rest of the SIMD matrix math seen here.
Even More redundant SIMD operations
There are useless vec4 × mat4 littered throughout the function, like here:
you might be surprised but this whole SIMD spaghetti can be reduced to just a single assignment:
Why?
The Mask_0010 vector value is (0, 0, 1, 0).
The code multiplies this mask by each row of the matrix:
- 0 * Row0 = Zero
- 0 * Row1 = Zero
- 1 * Row2 = Row2
- 0 * Row3 = Zero
Adding these together: Zero + Zero + Row2 + Zero = Row2.
This mask makes sure that only the 2nd row gets preserved and the rest get zeroed out.
Biggest reduction in SIMD operations:
Here is the biggest reduction in SIMD operations
From:
To:
- Mask_1000 is (1, 0, 0, 0)
- Mask_0100 is (0, 1, 0, 0)
- Mask_0010 is (0, 0, 1, 0)
Multiplying a unit vector by a matrix simply extracts the corresponding row. The original code was laboriously performing this extraction manually for each axis:
- The calculation for 0x240 used Mask_1000 to extract Row0.
- The calculation for 0x250 used Mask_0100 to extract Row1.
- The calculation for 0x260 used Mask_0010 to extract Row2.
We will Actually manually optimize SIMD assembly instructions to make use of this finding in the next post.
Continuaton of Manual Matrix Reconstruction
The last SIMD math operation we need to do before we get the entire ViewProjection Matrix is:
which is basically:
CamPos_Negated_w1_dup[Vec4] * VP_NoTrans[Matrix]
Let’s use our previous snapshot where:
Camera World Matrix:

ViewProjection Matrix (Without Translation):

- CamPos = [-112913.200, -613576.900, 2234.394, 1.00]
- CamPos_Negated = [112913.200, 613576.900, -2234.394, 1.00]
Now let’s multiply this negated camera position with the ViewProjection Matrix (without translation) to confirm if we get the full ViewProjection matrix:
Floating-point precision of 13 was used during multiplication to keep results accurate.

Last Row Matches Perfectly
The ViewProjection Matrix - Fully Reversed
Let’s Recap what we have uncovered by reversing the entire construction of the VP matrix down to its SIMD operations.
Our initial problem was straightforward:
Multiplying the View and Projection matrices directly did not produce the correct ViewProjection (VP) matrix used by the engine
After reversing and verifying, down to the SIMD instruction level, we discovered how the game actually constructs its View matrix from the Camera World matrix:
- Row[0] → becomes Column[2]
- Row[1] → becomes –Column[0]
- Row[2] → becomes Column[1]
- Row[3] → becomes (0, 0, 0, 1)
Once this View matrix is built, the engine multiplies it with the Projection matrix to produce an intermediate matrix, essentially the ViewProjection matrix without the translation component applied yet.
Finally, the engine takes this intermediate matrix and multiplies it with the negated camera position, producing the final ViewProjection matrix:
- Row[0] → becomes Column[2]
- Row[1] → becomes –Column[0]
- Row[2] → becomes Column[1]
- Row[3] → Computed as -dot(vec, CamPos)
Note: Multiplying the negated camera position with the ViewProjection matrix (without the translation component) is mathematically equivalent to –dot(vec, CamPos) as explained in part 4.2: Fast inverse for orthonormal Matrices
Final Verification:
Let’s take the Camera world Matrix:

And the Projection Matrix:

Trying to construct the intermediate Matrix (ViewProjection matrix without the translation) by following:
- Row[0] → becomes Column[2]
- Row[1] → becomes –Column[0]
- Row[2] → becomes Column[1]
- Row[3] → becomes (0, 0, 0, 1)
We get:
\[Intermediate Matrix = \begin{bmatrix} -0.906 & -0.072 & 0.416 & 0 \\ -0.423 & 0.154 & -0.893 & 0 \\ 0 & 0.985 & 0.170 & 0 \\ 0 & 0 & 0 & 1.0 \end{bmatrix}\]Multiply it with the projection Matrix:
\[\text{IntermediateMatrix} \times \text{ProjectionMatrix} = \begin{bmatrix} -0.906 & -0.072 & 0.416 & 0 \\ -0.423 & 0.154 & -0.893 & 0 \\ 0 & 0.985 & 0.170 & 0 \\ 0 & 0 & 0 & 1.0 \end{bmatrix} \times \begin{bmatrix} 1.264 & 0.000 & 0.000 & 0.000 \\ 0.000 & 2.247 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 1.000 \\ 0.000 & 0.000 & 10.000 & 0.000 \end{bmatrix}\]Result:
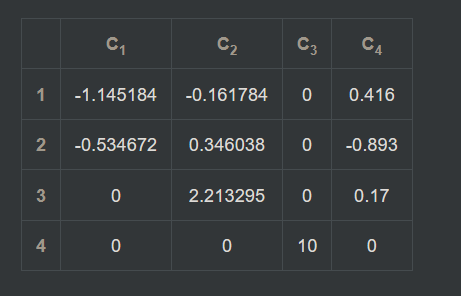
Comparing aganist in-game memory:

Great, It matches.
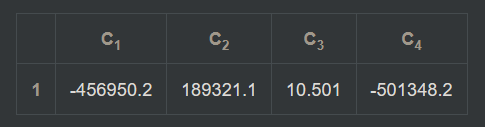
Next is multiplying the negated camera position with this Matrix:
\[\text{negCamPos} \times \text{ProjectionMatrix} = \begin{bmatrix} 112913.16 & 613576.88 & -2234.39 & 1 \end{bmatrix} \times \begin{bmatrix} -1.146 & -0.161 & 0.000 & 0.416 \\ -0.534 & 0.346 & 0.000 & -0.893 \\ 0.000 & 2.215 & 0.000 & 0.170 \\ 0.000 & 0.000 & 10.000 & 0.000 \end{bmatrix}\]Result:

Comparing against in-game memory:

Higher float presicon was used
Doing this in one Matrix Multiply we get a View Matrix that is built something like this:
\[\text{ViewMatrix} \times \text{ProjectionMatrix} = \begin{bmatrix} -u_x & f_x & r_x & 0 \\ -u_y & f_y & r_y & 0 \\ -u_z & f_z & r_z & 0 \\ dot(u, p) & -dot(f, p) & -dot(r, p) & 1.0 \end{bmatrix} \times \begin{bmatrix} 1.264 & 0.000 & 0.000 & 0.000 \\ 0.000 & 2.247 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 1.000 \\ 0.000 & 0.000 & 10.000 & 0.000 \end{bmatrix}\]Thus confriming that:
\[\text{ViewMatrix} \times \text{ProjectionMatrix} = \begin{bmatrix} -0.906 & -0.072 & 0.416 & 0 \\ -0.423 & 0.154 & -0.893 & 0 \\ 0 & 0.985 & 0.170 & 0 \\ -361842.34 & 84160.3 & -501332.11 & 1.0 \end{bmatrix} \times \begin{bmatrix} 1.264 & 0.000 & 0.000 & 0.000 \\ 0.000 & 2.247 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 1.000 \\ 0.000 & 0.000 & 10.000 & 0.000 \end{bmatrix}\]Gives us the Full View Projection Matrix:
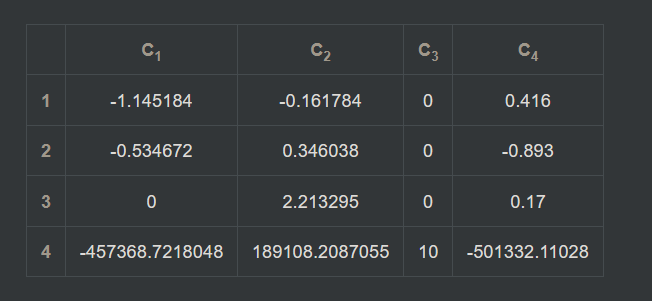
Camera World Matrix Does Not Match?
The camera world matrix we found was:
\[C_{world} = \begin{bmatrix} r_x & r_y & r_z & 0 \\ u_x & u_y & u_z & 0 \\ f_x & f_y & f_z & 0 \\ p_x & p_y & p_z & 1.0 \end{bmatrix}\]but it’s inverse is supposed to be:
\[C_{world}^{-1} = \begin{bmatrix} r_x & u_x & f_x & 0 \\ r_y & u_y & f_y & 0 \\ r_z & u_z & f_z & 0 \\ -dot(r, P) & -dot(u, P) & -dot(f, P) & 1.0 \end{bmatrix}\]However, the actual view matrix we recovered from the game looks very different:
\[\text{ViewMatrix} = \begin{bmatrix} -u_x & f_x & r_x & 0 \\ -u_y & f_y & r_y & 0 \\ -u_z & f_z & r_z & 0 \\ dot(u, p) & -dot(f, p) & -dot(r, p) & 1.0 \end{bmatrix}\]Whatever matrix the engine uses to position the camera in world space (the camera’s world matrix), its inverse must be the view matrix.
That’s absolute. So i’m sure the camera world matrix we found in memory was not infact the actual matrix used by the engine for it’s internal camera transform.
Instead, the engine likely uses this layout:
Applying the fast inverse formula:
\[C_{world}^{-1} = \begin{bmatrix} R^T & 0 \\ -TR^T & 1 \end{bmatrix}\]produces the exact view matrix used by the engine.
Thus pretty much confirming the Camera’s world matrix we found in memory is in a textbook layout and not the actual layout used for the camera transform.
In short, the camera world matrix doesn’t have to follow the textbook layout. As long as the engine is consistent in how it expects and inverts it, the result will always be valid.
Completion of VP matrix construction from SIMD operations
Thus completes the reconstruction of the ViewProjection matrix, starting from theoretical concepts, all the way to manual SIMD-level verification. Not only does this resolve the original discrepancy, but it also provides a concrete bridge between mathematical theory, graphics pipelines, and reverse engineering practice.
Next up: Trimming down redundant SIMD instructions using assembly patching and detour hooking. Don’t expect a real performance gain here, it’s more about recognizing wasted ops and experimenting with how far we can push the pipeline by hand.