Part 3: Finding & Reversing Matrices

How We Search for Matrices in Memory

A common approach is to switch Cheat Engine’s value type in float and then:

1. Look Directly up and scan for the value 1.0f.
2. Look Directly Down and scan for the value -1.0f.
3. Rescan to narrow the matrices down to matrices that are actively changing with camera orientation.

Once you narrow it down, you can inspect nearby memory regions and layout patterns (like a 4x4 float matrix) to identify which matrix it is

This technique works because these matrices are often stored in memory in a row-major or column-major 4x4 float array, and the directional vectors (Right, Up, Forward) reflect real-time camera movement

Basically Something in the matrix must encode the camera’s up/down rotation

Searching for Matrices in Ghost of Tsushima

Lets start searching for interesting matrices in memory in ghost of tsushima!

Looking up in game

Seraching for 1.0f in cheat engine

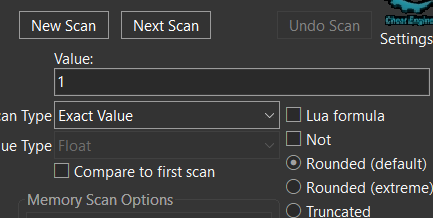
Now looking Down

Searching for -1.0f in cheat engine

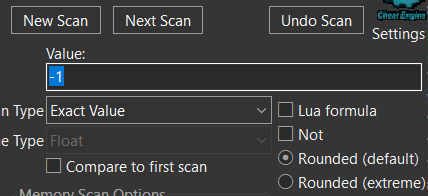
Now you’re going to get a lot of results. Keep refining your search (e.g., by changing camera angles and scanning again) until the number of results stabilizes and stops changing, that’s usually a good sign you’ve isolated the relevant addresses.

Now when reverse engineering a game, you’ll often find that the View, Projection, and View-Projection matrices (mostly) live at fixed or static memory addresses.
Why?
Mainly because these matrices are core components of the game’s rendering pipeline and are global to the camera or render context.

Now we can add all static memory address’s and browse its memory layout’s to see if we find some interesting matrices.

Like Here:

Here the first 4x4 matrix look like the Camera World Matrix and the second 4x4 matrix looks like the View Matrix.

Confirmation of the View and Camera World Matrices:

In Part 2.1: View Matrix we talked about the orthogonality and relations of the fundamental Vectors.
Let’s open these matrices in reclass and use these relations to confirm it!

Lets form an Hypothesis that this is the layout of the 4x4 Matrix:

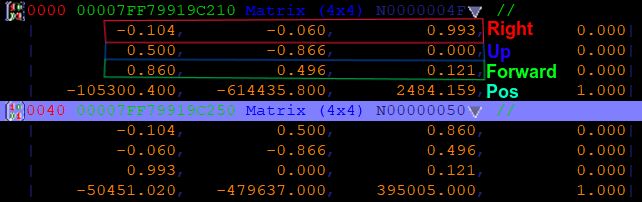
Using its relations we can see:

• Dot((-0.104, -0.06, 0.993), (0.5, -0.866, 0.00)) = -3.9999999999998E-5 which is basically just 0 and is just floating-point precision error.
• Cross((-0.104, -0.06, 0.993), (0.5, -0.866, 0.00)) = (0.860, 0.496, 0.121) which basically gave us the second row (starting row’s from 0)

This is handy in reverse engineering because you can’t always hope to stumble upon a perfect, clean 4×4 matrix in memory. Sometimes you’ll just find a couple of direction vectors (like Right and Up) sitting in random spots or being passed into a function. With some quick vector math, you can fill in the missing one using a cross product, or sanity-check them with a dot product (should be zero if they’re perpendicular). That way, even if the layout is weird or partially obfuscated, you can still piece it together.
Also Handy if you are not sure if this ViewMatrix is not altered in any way eg: Its the Model-View Matrix.

If the values are orthogonal, have unit lengths, include a clear translation component (usually the bigger numbers > 1.0f), and end with the homogeneous coordinate row or column [0, 0, 0, 1], you can be pretty sure it’s a real transformation matrix.

To be extra sure, don’t just trust the layout you find. The 0th row isn’t always Right and the last row isn’t always Translation. It’s usually textbook layout in most games, but not always. Move the camera around and watch which parts of the matrix change. Let the behavior tell you what’s what.

Lets now inverse it to get the view matrix:

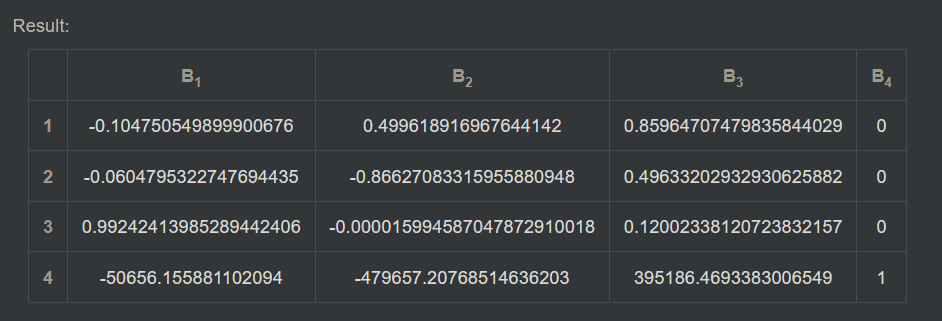
We can see it exactly matches the second 4x4 matrix we see in memory (Camera World Matrix (Inverse) = View Matrix).

We can also take dot(Right, Pos) and compare it against the translation component of the second matrix as another way to confirm this relationship.

Thus pretty much confirming the first matrix to be Camera World Matrix and the second matrix to be the View Matrix.

Looking at other matrices

Here we see some other matrices:

The first matrix clearly resembles a projection matrix, but in this case, it uses a reverse-Z projection setup meaning the depth range is inverted so that the near plane maps to 1.0 and the far plane maps to 0.0.

The second matrix appears to be the View-Projection (VP) matrix, produced by multiplying the Projection and View matrices together.

The third matrix appears to be the View-Projection matrix but with the translation component zeroed out.

Why?
Because they fit the general layout’s expected of these matrices.
To be sure lets plug in the view projection matrix into a world to screen function to see if we can confirm this.

To verify i will manually input the entity coordinates into my world to screen program.
Here is the entity whose position we’ll convert:

Since this image shows that the entity is at the top-left corner of our screen at a resolution of 1920x1080 we can expect the screen coordinates to be close to (0, 0) since the Top-left corner is the origin of the screen (0, 0), not bottom left as you might expect (unlike OpenGL).

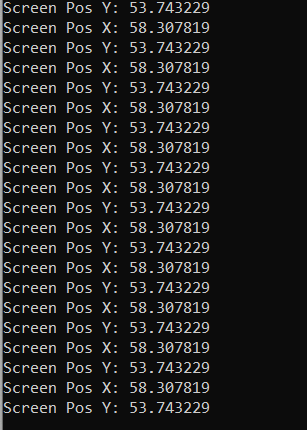
Here we can see the output screen coordinates matches closely to what we expected.

We’ll cover how to get the entity’s 3D coordinates and how World-to-Screen works in detail later, for now, this confirms the matrix is correct.

Quick Note: The top left is (0,0) for Direct-X in the context of Screen Space Coordinates but for Normalized Device Coordinates (NDC) the center of the screen is (0,0) and the top left would be (-1,1).

Other ways to get the VP matrix

You don’t have to rely on pure luck to find the VP matrix. Instead of just stumbling across it, you can track it down by first finding the camera world matrix, view matrix, or projection matrix, then checking which functions access these matrices.

When digging through those functions in IDA, look for clues like:

• Expected function arguments: e.g., does the function take both a View Matrix and a Projection Matrix?
• SIMD-heavy math patterns: Does the function use SIMD math for matrix multiplication?
• Matrix usage: Which matrices does it load for its calculations?
• Inverse operations: Is it inverting the camera world matrix at any point?

Example:

I used this method to identify the VP matrix construction function in a Denuvo protected game, Ghost Recon Wildlands. I looked at what accessed the projection matrix and found the function that builds the VP matrix.

Dealing with Denuvo’s anti-reverse engineering tricks and other protections felt like i was doing a lobotomy speedrun any%.
If you ever want to test your sanity, try reversing a Denuvo game.

Trying to Rebuild the View-Projection Matrix

Now that we have confirmed that this is in fact the view projection matrix lets try to reconstruct it manually

1. Take the inverse of the Camera World Matrix
2. Multiply it with the suspected Projection Matrix

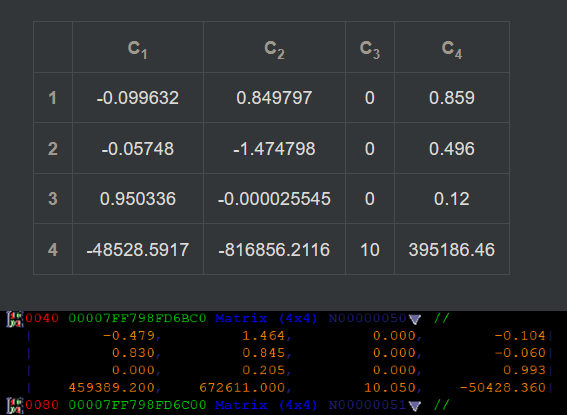
Here for some reason it doesn’t quite match’s up although quite similar.

Next Step: Time to start tracing back the functions that write to the final View-Projection Matrix in memory.